Точечная нотация

При реализации Лиспа в качестве единой универсальной базовой структуры для конструирования символьных выражений использовалась так называемая "точечная нотация" (dot-nоtation), согласно которой левая и правая части бинарного узла равноправны и могут хранить данные любой природы.

Бинарный узел, содержащий пару атомов ATOM1 и ATOM2,

можно представить как запись вида:

( ATOM1 . ATOM2 )

Если вместо атомов "ATOM1", "ATOM2" рекурсивно подставлять произвольные атомы, затем построенные из них пары и так далее, то мы получим множество всех возможных составных символьных выражений – S-выражений.

S-выражение - это или атом или заключенная в скобки пара из двух S-выражений, разделенных точкой.

Все сложные данные создаются из одинаково устроенных блоков - бинарных узлов, содержащих пары объектов произвольного вида. Каждый бинарный узел соответствует минимальному блоку памяти.

Списки – это подмножество S-выражений, движение вправо по которым завершается атомом Nil.

(A . B)

(C . (A . B))

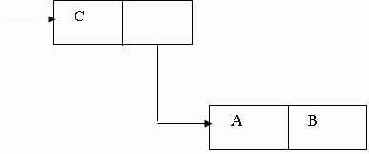
Пример 3.3.

(html, txt)

Любое S-выражение может быть построено из атомов с помощью CONS и любая его часть может быть выделена с помощью CAR-CDR.

Упражнение 3.3. Нарисуйте диаграммы для следующих S-выражений:

((A . B) . C) ((A . B) . (D . C)) ((A . B) . (D . (C . E)))

Точечная нотация может точно представлять логику хранения любых структур данных в памяти и доступа к компонентам структур данных. В виде списков можно представить лишь те S-выражения, в которых при движении вправо в конце концов обнаруживается атом Nil, символизирующий завершение списка.

Упражнение 3.4. Посмотрите, что делает Лисп-система с ниже приведенными выражениями, сравнивая результаты с данными из таблицы 3.2:

(CONS 'Head 'Tail ) (CAR '(Head . Tail)) (CDR '(Head . Tail)) (ATOM 'Atom) (ATOM ()) (ATOM (CAR '(Head . Tail))) (EQ Nil ())

Атом Nil, рассматриваемый как представление пустого списка (), выполняет роль ограничителя в списках. Одноэлементный список (A) идентичен S-выражению (A . Nil). Список (A1 A2 … Ak) может быть представлен как S-выражение вида:

(A1 . (A2 . ( … . (Ak . Nil) … ))).

В памяти это фактически одна и та же структура данных.

Таблица 3.3. Соответствие списков и равнозначных им S-выраженийList-notation - списочная запись объектаDot-notation - точечная запись того же объекта

(A B C )	(A . (B . (C . Nil)))
((A B) C )	((A . (B . Nil)) . (C . Nil))
(A B (C E))	(A . (B . ((C . (E . Nil)). Nil)))
(A)	(A . Nil)
((A))	((A . Nil) . Nil
(A (B . C))	(A . ((B . C) . Nil))
(())	(Nil . Nil)
(A B . C)	(A . (B . C))

Для многошагового доступа к отдельным элементам такой структуры удобно пользоваться мнемоническими обозначениями композиций из многократных CAR-CDR. Имена таких композиций устроены как цепочки из "a" или "d", задающие маршрут движения из шагов CAR и CDR соответственно, расположенный между "c" и "r". Указанные таким способом CAR-CDR исполняются с ближайшего к аргументу шага, т.е. в порядке, обратном записи.

Таблица 3.4. Примеры многошагового доступа к элементам структуры.Композиции CAR-CDRВычисляются в порядке, обратном записи:

CAAR	((A ) B C)	A
CADR	(A B C)	B - CDR, затем CAR
CADDR	(A B C)	C - (дважды CDR), затем CAR
CADADR	(A (B C) D)	C - два раза:(CDR, затем CAR)

Упражнение 3.5. Посмотрите, что делает Лисп-система с ниже приведенными выражениями, сравнивая результаты с данными из таблицы 3.3:

(cAAr '((A) B C) ) (cADr '(A B C)) (cADDr '(A B C) ) (cADADr '(A (B C) D)) Таблица 3.5. Clisp: Функции для работы с данными

(Append Список … )	Сцепляет списки, полученные как аргументы
(Assoc Атом А-список)	Находит в А- списке пару, левая часть которой – Атом
Atom	Проверка на атомарность
Car	Первый элемент списка или левый элемент структуры
Cdr	Результат удаления первого элемена из списка или правый элемент структуры
Cons	Создание узла из двух элементов
(Eq Данное1 Данное2)	Истина при идентичных данных
(Equal Структура1 Структура2 )	Истина при эквивалентных структурах
(Delete Объект Список )	Строит копию Списка без заданного объекта
(Intersection Список … )	Пересечение списков
(Last Список )	Последний элемент структуры, представляющей список. Можно задавать длину завершающего отрезка списка.
(Lenth Список )	Длина списка
(List Форма … )	Строит список из значений Форм
(Member Объект Список )	Ищет Объект в Списке
(Null Форма)	Истина для Nil
(Pairlis Атомы Данные А-спиок)	Пополняет А-список парами из Атомов и значений, соответствующих Данных.
(Reverse Список )	Копия Списка с обратным порядком элементов
(Set-difference Список … )	Разность множеств, представленных Списками
(Sort Список Предикат )	Упорядочивает Список согласно Предикату
(Sublis А-список Структура )	Преобразует Структуру согласно А-списку методом подстановки данных вместо связанных с ними атомов.
(Subst Новое Старое Структура )	Преобразует Структуру, заменяя Старое на Новое.
(Union Список … )	Объединение множеств, представленных Списками.

Содержание раздела